| A | B | A ∨ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| A | B | A ∧ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | 〜A |
|---|---|
| 0 | 1 |
| 1 | 0 |
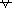 Bの真理値表
Bの真理値表
| A | B | A 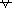 B B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1+2=3 : | 真の値をとる命題 |
| 1+1=3 : | 偽の値をとる命題 |
| 3は素数である : | 真の値をとる命題 |
| 最小の素数: | 命題でない(真・偽以外の値) |
| 明日は雨でしょう: | 命題でない(真・偽が不明) |
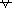 B:「今日の天気は雨、または、風が強いかのどちら一方である」
B:「今日の天気は雨、または、風が強いかのどちら一方である」
(1)A ∨ Bの真理値表
|
(2)A ∧ Bの真理値表
| ||||||||||||||||||||||||||||||
(3)〜Aの真理値表
|
(4)A 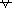 Bの真理値表 Bの真理値表
|
| (1)べき等則 | A∨A= A, A∧A= A |
| (2)交換則 | A∨B= B∨A, A∧B= B∧A |
| (3)分配則 | A∧(B∨C)= (A∧B)∨(A∧C) A∨(B∧C)= (A∨B)∧(A∨C) |
| (4)結合則 | (A∨B)∨C= A∨(B∨C) (A∧B)∧C= A∧(B∧C) |
| (5)吸収則 | A∨(A∧B)= A A∧(A∨B)=A |
| (6)その他 | A∨1= 1, A∧1=A A∨0= A, A∧0=0 A∨〜A= 1, A∧〜A=0 |
| (7)ド・モルガンの定理 | 〜(A∨B)= 〜A∧〜B 〜(A∧B)= 〜A∨〜B |